Фильтр Калмана

Фильтр Калмана широко используется в инженерных и эконометрических приложениях: от радаров и систем технического зрения до оценок параметров макроэкономических моделей . Калмановская фильтрация является важной частью теории управления , играет большую роль в создании систем управления. Совместно с линейно-квадратичным регулятором фильтр Калмана позволяет решить задачу линейно-квадратичного гауссовского управления . Фильтр Калмана и линейно-квадратичный регулятор - возможное решение большинства фундаментальных задач в теории управления.

В большинстве приложений количество параметров, задающих состояние объекта, больше, чем количество наблюдаемых параметров, доступных для измерения. При помощи модели объекта по ряду доступных измерений фильтр Калмана позволяет получить оценку внутреннего состояния.

Фильтр Калмана предназначен для рекурсивного дооценивания вектора состояния априорно известной динамической системы, то есть для расчёта текущего состояния системы необходимо знать текущее измерение, а также предыдущее состояние самого фильтра. Таким образом, фильтр Калмана, как и множество других рекурсивных фильтров, реализован во временно́м, а не в частотном представлении.

Наглядный пример возможностей фильтра - получение точных, непрерывно обновляемых оценок положения и скорости некоторого объекта по результатам временно́го ряда неточных измерений его местоположения. Например, в радиолокации стоит задача сопровождения цели, определения её местоположения, скорости и ускорения, при этом результаты измерений поступают постепенно и сильно зашумлены. Фильтр Калмана использует вероятностную модель динамики цели, задающую тип вероятного движения объекта, что позволяет снизить воздействие шума и получить хорошие оценки положения объекта в настоящий, будущий или прошедший момент времени.

Введение

Фильтр Калмана оперирует понятием вектора состояния системы (набором параметров, описывающих состояние системы на некоторый момент времени) и его статистическим описанием. В общем случае динамика некоторого вектора состояния описывается плотностями вероятности распределения его компонент в каждый момент времени. При наличии определенной математической модели производимых наблюдений за системой, а также модели априорного изменения параметров вектора состояния (а именно - в качестве марковского формирующего процесса) можно записать уравнение для апостериорной плотности вероятности вектора состояния в любой момент времени. Данное дифференциальное уравнение носит название уравнение Стратоновича. Уравнение Стратоновича в общем виде не решается. Аналитическое решение удается получить только в случае ряда ограничений (предположений):

• гауссовости априорных и апостериорных плотностей вероятности вектора состояния на любой момент времени (в том числе начальный)
• гауссовости формирующих шумов
• гауссовости шумов наблюдений
• белости шумов наблюдений
• линейности модели наблюдений
• линейности модели формирующего процесса (который, напомним, должен являться марковским процессом)

Классический фильтр Калмана является уравнениями для расчета первого и второго момента апостериорной плотности вероятности (в смысле вектора математических ожиданий и матрицы дисперсий, в том числе взаимных) при данных ограничениях. Ввиду того, что для нормальной плотности вероятности математическое ожидание и дисперсионная матрица полностью задают плотность вероятности, можно сказать, что фильтр Калмана рассчитывает апостериорную плотность вероятности вектора состояния на каждый момент времени. А значит полностью описывает вектор состояния как случайную векторную величину.

Расчетные значения математических ожиданий при этом являются оптимальными оценками по критерию среднеквадратической ошибки, что и обуславливает его широкое применение.

Существует несколько разновидностей фильтра Калмана, отличающихся приближениями и ухищрениями, которые приходится применять для сведения фильтра к описанному виду и уменьшения его размерности:

• Расширенный фильтр Калмана (EKF, Extended Kalman filter). Сведение нелинейных моделей наблюдений и формирующего процесса с помощью линеаризации посредством разложения в ряд Тейлора .
• Unscented Kalman filter (UKF). Используется в задачах, в которых простая линеаризация приводит к уничтожению полезных связей между компонентами вектора состояния. В этом случае «линеаризация» основана на unscented -преобразовании.
• Ensemble Kalman filter (EnKF). Используется для уменьшения размерности задачи.
• Возможны варианты с нелинейным дополнительным фильтром, позволяющим привести негауссовские наблюдения к нормальным.
• Возможны варианты с «обеляющим» фильтром, позволяющим работать с «цветными» шумами
• и т. д.

Используемая модель динамической системы

Фильтры Калмана базируются на дискретизированных по времени линейных динамических системах . Такие системы моделируются цепями Маркова при помощи линейных операторов и слагаемых с нормальным распределением . Состояние системы описывается вектором конечной размерности - вектором состояния . В каждый такт времени линейный оператор действует на вектор состояния и переводит его в другой вектор состояния (детерминированное изменение состояния), добавляется некоторый вектор нормального шума (случайные факторы) и в общем случае вектор управления, моделирующий воздействие системы управления. Фильтр Калмана можно рассматривать как аналог скрытым моделям Маркова , с тем отличием, что переменные, описывающие состояние системы, являются элементами бесконечного множества действительных чисел (в отличие от конечного множества пространства состояний в скрытых моделях Маркова). Кроме того, скрытые модели Маркова могут использовать произвольные распределения для последующих значений вектора состояния, в отличие от фильтра Калмана, использующего модель нормально распределенного шума. Существует строгая взаимосвязь между уравнениями фильтра Калмана и скрытой модели Маркова. Обзор этих и других моделей дан Roweis и Chahramani (1999) .

При использовании фильтра Калмана для получения оценок вектора состояния процесса по серии зашумленных измерений необходимо представить модель данного процесса в соответствии со структурой фильтра - в виде матричного уравнения определенного типа. Для каждого такта k работы фильтра необходимо в соответствии с приведенным ниже описанием определить матрицы: эволюции процесса F k ; матрицу наблюдений H k ; ковариационную матрицу процесса Q k ; ковариационную матрицу шума измерений R k ; при наличии управляющих воздействий - матрицу их коэффициентов B k .

Иллюстрация работы фильтра. Квадратами помечены матрицы . Эллипсами помечены матрицы многомерных нормальных распределений (включая средние значения и ковариации). Не обведёнными оставлены векторы . В простейшем случае некоторые матрицы не изменяются во времени (не зависят от индекса k ), но всё равно используются фильтром в каждый такт работы.

Модель системы/процесса подразумевает, что истинное состояние в момент k получается из истинного состояния в момент k −1 в соответствии с уравнением:

,

• F k - матрица эволюции процесса/системы, которая воздействует на вектор x k −1 (вектор состояния в момент k −1 );
• B k - матрица управления, которая прикладывается к вектору управляющих воздействий u k ;
• w k - нормальный случайный процесс с нулевым математическим ожиданием и ковариационной матрицей Q k , который описывает случайный характер эволюции системы/процесса:

В момент k производится наблюдение (измерение) z k истинного вектора состояния x k , которые связаны между собой уравнением:

где H k - матрица измерений, связывающая истинный вектор состояния и вектор произведенных измерений, v k - белый гауссовский шум измерений с нулевым математическим ожиданием и ковариационной матрицей R k :

Начальное состояние и векторы случайных процессов на каждом такте {x 0 , w 1 , …, w k , v 1 , …, v k } считаются независимыми .

Многие реальные динамические системы нельзя точно описать данной моделью. На практике неучтённая в модели динамика может серьёзно испортить рабочие характеристики фильтра, особенно при работе с неизвестным стохастическим сигналом на входе. Более того, неучтённая в модели динамика может сделать фильтр неустойчивым . С другой стороны, независимый белый шум в качестве сигнала не будет приводить к расхождению алгоритма. Задача отделения шумов измерений от неучтенной в модели динамики сложна, решается она с помощью теории робастных систем управления .

Фильтр Калмана

Фильтр Калмана является разновидностью рекурсивных фильтров . Для вычисления оценки состояния системы на текущий такт работы ему необходима оценка состояния (в виде оценки состояния системы и оценки погрешности определения этого состояния) на предыдущем такте работы и измерения на текущем такте. Данное свойство отличает его от пакетных фильтров, требующих в текущий такт работы знание истории измерений и/или оценок. Далее под записью будем понимать оценку истинного вектора в момент n с учетом измерений с момента начала работы и по момент m включительно.

Состояние фильтра задается двумя переменными:

Итерации фильтра Калмана делятся на две фазы: экстраполяция и коррекция. Во время экстраполяции фильтр получает предварительную оценку состояния системы (в русскоязычной литературе часто обозначается , где означает «экстраполяция», а k - номер такта, на котором она получена) на текущий шаг по итоговой оценке состояния с предыдущего шага (либо предварительную оценку на следующий такт по итоговой оценке текущего шага, в зависимости от интерпретации). Эту предварительную оценку также называют априорной оценкой состояния, так как для её получения не используются наблюдения соответствующего шага. В фазе коррекции априорная экстраполяция дополняется соответствующими текущими измерениями для коррекции оценки. Скорректированная оценка также называется апостериорной оценкой состояния, либо просто оценкой вектора состояния . Обычно эти две фазы чередуются: экстраполяция производится по результатам коррекции до следующего наблюдения, а коррекция производится совместно с доступными на следующем шаге наблюдениями, и т. д. Однако возможно и другое развитие событий, если по некоторой причине наблюдение оказалось недоступным, то этап коррекции может быть пропущен и выполнена экстраполяция по нескорректированной оценке (априорной экстраполяции). Аналогично, если независимые измерения доступны только в отдельные такты работы, всё равно возможны коррекции (обычно с использованием другой матрицы наблюдений H k ).

Этап экстраполяции

Этап коррекции

Отклонение полученного на шаге k наблюдения от наблюдения, ожидаемого при произведенной экстраполяции:
Ковариационная матрица для вектора отклонения (вектора ошибки):
Оптимальная по Калману матрица коэффициентов усиления, формирующаяся на основании ковариационных матриц имеющейся экстраполяции вектора состояния и полученных измерений (посредством ковариационной матрицы вектора отклонения):
Коррекция ранее полученной экстраполяции вектора состояния - получение оценки вектора состояния системы:
Расчет ковариационной матрицы оценки вектора состояния системы:

Выражение для ковариационной матрицы оценки вектора состояния системы справедливо только при использовании приведенного оптимального вектора коэффициентов. В общем случае это выражение имеет более сложный вид.

Инварианты

Если модель абсолютно точна и абсолютно точно заданы начальные условия и , то следующие величины сохраняются после любого количества итераций работы фильтра - являются инвариантами:

Математические ожидания оценок и экстраполяций вектора состояния системы, матрицы ошибок являются нуль-векторами:

где - математическое ожидание .

Расчетные матрицы ковариаций экстраполяций, оценок состояния системы и вектора ошибок совпадают с истинными матрицами ковариаций:

Пример построения фильтра

Представим себе вагонетку , стоящую на бесконечно длинных рельсах при отсутствии трения . Изначально она покоится в позиции 0, но под действием случайных факторов на неё действует случайное ускорение . Мы измеряем положение вагонетки каждые ∆t секунд, но измерения неточны. Мы хотим получать оценки положения вагонетки и её скорости. Применим к этой задаче фильтр Калмана, определим все необходимые матрицы.

В данной задаче матрицы F , H , R и Q не зависят от времени, опустим их индексы. Кроме того, мы не управляем вагонеткой, поэтому матрица управления B отсутствует.

Координата и скорость вагонетки описывается вектором в линейном пространстве состояний

где - скорость (первая производная координаты по времени).

Будем считать, что между (k −1 )-ым и k -ым тактами вагонетка движется с постоянным ускорением a k , распределенным по нормальному закону с нулевым математическим ожиданием и среднеквадратическим отклонением σ a . В соответствии с механикой Ньютона можно записать

.

Ковариационная матрица случайных воздействий

(σ a - скаляр).

На каждом такте работы производится измерение положения вагонетки. Предположим, что погрешность измерений v k имеет нормальное распределение с нулевым математическим ожиданием и среднеквадратическим отклонением σ z . Тогда

и ковариационная матрица шума наблюдений имеет вид

.

Начальное положение вагонетки известно точно

, .

Если же положение и скорость вагонетки известна лишь приблизительно, то можно инициализировать матрицу дисперсий достаточно большим числом L , чтобы при этом число превосходило дисперсию измерений координаты

, .

В этом случае на первых тактах работы фильтр будет с бо́льшим весом использовать результаты измерений, чем имеющуюся априорную информацию.

Вывод формул

Ковариационная матрица оценки вектора состояния

По определению ковариационной матрицы P k |k

подставляем выражение для оценки вектора состояния

и расписываем выражение для вектора ошибок

и вектора измерений

выносим вектор погрешности измерений v k

так как вектор погрешности измерений v k не коррелирован с другими аргументами, получаем выражение

в соответствии со свойствами ковариации векторов данное выражение преобразуется к виду

заменяя выражение для ковариационной матрицы экстраполяции вектора состояния на P k |k −1 и определение ковариационной матрицы шумов наблюдений на R k , получаем

Полученное выражение справедливо для произвольной матрицы коэффициентов, но если в качестве неё выступает матрица коэффициентов, оптимальная по Калману, то данное выражение для ковариационной матрицы можно упростить.

Оптимальная матрица коэффициентов усиления

Фильтр Калмана минимизирует сумму квадратов математических ожиданий ошибок оценки вектора состояния.

Вектор ошибки оценки вектора состояния

Стоит задача минимизировать сумму математических ожиданий квадратов компонент данного вектора

,

что эквивалентно минимизации следа ковариационной матрицы оценки вектора состояния P k |k . Подставим в выражение для ковариационной матрицы оценки вектора состояния имеющиеся выражения и дополним до полного квадрата:

Заметим что, последнее слагаемое является ковариационной матрицей некоторой случайной величины, поэтому его след неотрицателен. Минимум следа достигнется при обнулении последнего слагаемого:

Утверждается, что данная матрица является искомой и при использовании в качестве матрицы коэффициентов в фильтре Калмана минимизирует сумму средних квадратов ошибок оценки вектора состояния.

Ковариационная матрица оценки вектора состояния при использовании оптимальной матрицы коэффициентов

Выражение для ковариационной матрицы оценки вектора состояния P k |k при использовании оптимальной матрицы коэффициентов примет вид:

Данная формула вычислительно проще и поэтому практически всегда используется на практике, но она корректна только при использовании оптимальной матрицы коэффициентов. Если ввиду малой вычислительной точности возникает проблема с вычислительной устойчивостью, либо специально используется матрица коэффициентов, отличная от оптимальной, следует использовать общую формулу для ковариационной матрицы оценки вектора состояния.

Как то так повелось, что очень нравятся мне всякие алгоритмы, имеющие четкое и логичное математическое обоснование) Но зачастую их описание в интернете настолько перегружено формулами и расчетами, что общий смысл алгоритма понять просто невозможно. А ведь понимание сути и принципа работы устройства/механизма/алгоритма намного важнее, чем заучивание огромных формул. Как это ни банально, но запоминание даже сотни формул ничем не поможет, если не знать, как и где их применить 😉 Собственно, к чему все это.. Решил я замутить описание некоторых алгоритмов, с которыми мне приходилось сталкиваться на практике. Постараюсь не перегружать математическими выкладками, чтобы материал был понятным, а чтение легким.

И сегодня мы поговорим о фильтре Калмана , разберемся, что это такое, для чего и как он применяется.

Начнем с небольшого примера. Пусть перед нами стоит задача определять координату летящего самолета. Причем, естественно, координата (обозначим ее ) должна определяться максимально точно.

На самолете мы заранее установили датчик, который и дает нам искомые данные о местоположении, но, как и все в этом мире, наш датчик неидеален. Поэтому вместо значения мы получаем:

где – ошибка датчика, то есть случайная величина. Таким образом, из неточных показаний измерительного оборудования мы должны получить значение координаты (), максимально близкое к реальному положению самолета.

Задача поставлена, перейдем к ее решению.

Пусть мы знаем управляющее воздействие (), благодаря которому летит самолет (пилот сообщил нам, какие рычаги он дергает 😉). Тогда, зная координату на k-ом шаге, мы можем получить значение на (k+1) шаге:

Казалось бы, вот оно, то что надо! И никакой фильтр Калмана тут не нужен. Но не все так просто.. В реальности мы не можем учесть все внешние факторы, влияющие на полет, поэтому формула принимает следующий вид:

где – ошибка, вызванная внешним воздействием, неидеальностью двигателя итп.

Итак, что же получается? На шаге (k+1) мы имеем, во-первых, неточное показание датчика , а во-вторых, неточно рассчитанное значение , полученное из значения на предыдущем шаге.

Идея фильтра Калмана заключается в том, чтобы из двух неточных значений (взяв их с разными весовыми коэффициентами) получить точную оценку искомой координаты (для нашего случая). В общем случае, измеряемая величина можем быть абсолютно любой (температура, скорость..). Вот, что получается:

Путем математических вычислений мы можем получить формулу для расчета коэффициента Калмана на каждом шаге, но, как условились в начале статьи, не будем углубляться в вычисления, тем более, что на практике установлено, что коэффициент Калмана с ростом k всегда стремится к определенному значению. Получаем первое упрощение нашей формулы:

А теперь предположим, что связи с пилотом нет, и мы не знаем управляющее воздействие . Казалось бы, в этом случае фильтр Калмана мы использовать не можем, но это не так 😉 Просто “выкидываем” из формулы то, что мы не знаем, тогда

Получаем максимально упрощенную формулу Калмана, которая тем не менее, несмотря на такие “жесткие” упрощения, прекрасно справляется со своей задачей. Если представить результаты графически, то получится примерно следующее:

Если наш датчик очень точный, то естественно весовой коэффициент K должен быть близок к единице. Если же ситуация обратная, то есть датчик у нас не очень хороший, то K должен быть ближе к нулю.

На этом, пожалуй, все, вот так вот просто мы разобрались с алгоритмом фильтрации Калмана! Надеюсь, что статья оказалась полезной и понятной =)

Транскрипт

1 # 09, сентябрь 2015 УДК Применение фильтра Калмана для обработки последовательности GPS-координат Листеренко Р.Р., бакалавр Россия, г. Москва, МГТУ им. Н.Э. Баумана, кафедра «Программное обеспечение ЭВМ и информационные технологии» Научный руководитель: Бекасов Д.Е., ассистент Россия, г. Москва, МГТУ им. Н.Э. Баумана, кафедра «Программное обеспечение ЭВМ и информационные технологии» Задача фильтрации GPS-координат В настоящее время широко используются сервисы GPS-трекинга, задачей которых является отслеживание маршрутов наблюдаемых объектов с целью их сохранения и дальнейшего воспроизведения и анализа. Однако из-за погрешности GPS-датчика, обусловленной рядом причин , таких как потеря сигнала от спутника, изменение геометрии расположения спутников, отражение сигналов, вычислительные ошибки и ошибки округления, итоговый результат не соответствует в точности маршруту объекта. Наблюдаются как незначительные отклонения (в пределах 100 м), не затрудняющие восприятие визуальной информации о маршруте и его анализ, так и весьма значительные (до 1 км, в случае потери сигнала спутников и использования базовых станций до нескольких десятков км). Для демонстрации результата приведенного в статье алгоритма используется маршрут, содержащий отклонения от действительного местоположения, превышающие несколько километров. С целью коррекции таких погрешностей разрабатывается алгоритм, выполняющий преобразование последовательности координат. Входными данными для алгоритма служит последовательность GPS-координат. В каждой координате содержится следующая информация, полученная от датчика: Широта Долгота Азимут в градусах Мгновенная скорость объекта в данной точке в м/с

2 Возможное отклонение координат объекта от истинного значения в метрах Время получения координаты датчиком Результатом работы алгоритма является последовательность координат с скорректированной широтой и долготой. В качестве основы для построения алгоритма решено использовать фильтр Калмана, так как он позволяет отдельно учитывать погрешности измерений и погрешности случайного процесса, а также использовать получаемую от датчика скорость движения объекта . Построение математической модели с использованием фильтра Калмана Для использования фильтра Калмана необходимо, чтобы исследуемый процесс описывался следующим образом : = + + (1) = + (2) В формуле (1) - вектор состояния процесса, A - матрица размерностью n n, описывающая переход наблюдаемого процесса из состояния в состояние. Вектор описывает управляющие воздействия на процесс. Матрица B размерностью n l отображает вектор управляющих воздействий u в изменение состояния s. является случайной величиной, описывающей погрешности исследуемого процесса, причем ~0, где Q - ковариационная матрица погрешностей процесса. Формула (2) описывает измерения случайного процесса. - вектор измеряемого состояния процесса, матрица H размерностью m n отображает состояние процесса в измерение процесса. - случайная величина, характеризующая погрешности измерений, причем ~0, где P - ковариационная матрица погрешностей измерений. Так как исследуется процесс движения объекта, уравнение состояния составляется исходя из уравнения движения тела = + +!" #$ % & ". Кроме того, отсутствует дополнительная информация о процессе движения, поэтому считается, что управляющее воздействие равно 0. За состояние процесса принят вектор = + () *, -. +, где x, y - координаты объекта, - проекции скорости объекта. Таким образом, для рассматриваемого процесса уравнение (1) принимает следующий вид: = + /!, (3) Молодежный научно-технический вестник ФС, ISSN

3 где = ! = 3! + 7 " 0 ; 6 2: 6 " / = : 6 0: 6 2: 6 0: , (4)!,4, (5) (6) В данной модели ускорение объекта рассматривается как случайная погрешность процесса. Принимаются следующие допущения: а) Ускорения по разным осям являются независимыми случайными величинами.),* б)

4 = AB = C. C E. = C/!!. /. = / C!!. /. Так как компоненты вектора ak (5) являются независимыми случайными величинами, то C!!. = " 0 " G. Следовательно, формула (7) принимает следующий вид: = / " (8) Вектор измерения zk для данной задачи представляется следующим образом: H I = 0 + J, J (7) 2, (9) где H, I - координаты объекта, полученные от датчика, J +,J, - скорость объекта, полученная от датчика. Матрица H в формуле (2) принимается равной единичной матрице размерностью 4 4, так как в рамках данной задачи считается, что измерение есть линейная комбинация вектора состояния и некоторых случайных погрешностей. Ковариационная матрица погрешности измерений R считается заданной. Один из возможных вариантов ее вычисления - использование данных о предполагаемой точности измерения, получаемых от датчика. Применение фильтра Калмана к построенной модели Для применения фильтра необходимо ввести следующие понятия: - апостериорная оценка состояния объекта в момент k, полученная по результатам наблюдений вплоть до момента k включительно. L - нескорректированная апостериорная оценка состояния объекта в момент времени k. - апостериорная ковариационная матрица ошибок, задающая оценку точности полученной оценки вектора состояния и включающая в себя оценку дисперсий погрешности вычисленного состояния и ковариации, показывающие выявленные взаимосвязи между параметрами состояния системы. L - нескорректированная апостериорная ковариационная матрица ошибок. Матрица P0 задается как нулевая, так как считается, что известно начальное положение объекта. Молодежный научно-технический вестник ФС, ISSN

5 Одна итерация фильтра Калмана состоит из двух этапов: экстраполяция и коррекция. а) На этапе экстраполяции вычисляется оценка L по оценке вектора состояния L и ковариационная матрица ошибок L по следующим формулам: L =, (10) L =. +, (11) где матрица Ak известна из формулы (4), матрица Qk вычисляется по формуле (8). б) На этапе коррекции вычисляется матрица коэффициентов усиления Kk по следующей формуле: M = L. L. + (12) где R, H считаются известными. Kk используется для коррекции оценки состояния объекта L и ковариационной матрицы ошибок L следующим образом: = L + M L, (13) = N M L, (14) где I - единичная матрица. Следует заметить, что для использования указанных выше соотношений, необходимо, чтобы для параметров объекта, участвующих в вычислениях, единицы измерений были согласованы. Однако в исходных данных широта и долгота приводятся в угловых координатах, а скорость в метрических. Кроме того, ускорение для расчета ошибки процесса также удобнее задавать в метрических единицах. Для перевода скорости и ускорения в угловые единицы используются формулы Винченти . Результат работы фильтра На рис. 1 приведен пример маршрута до обработки. Можно заметить, что в данном примере присутствуют несколько координат с высокой степенью погрешности, что выражается в наличии «пиков» координат, значительно удаленных от основного маршрута. На рис. 2 приведен результат работы фильтра с данным маршрутом.

6 Рис. 1. Маршрут объекта Рис. 2. Маршрут объекта после применения фильтра В результате практически отсутствуют «пики», за исключением самого крупного, который был заметно уменьшен, и сглажена остальная часть маршрута. Таким образом, с помощью приведенного алгоритма удалось снизить степень искажений маршрута и повысить его визуальное качество. Заключение В данной работе был рассмотрен подход к коррекции GPS-координат с помощью фильтра Калмана. С помощью приведенного алгоритма удалось устранить наиболее заметные искажения маршрута, что демонстрирует применимость данного метода к задаче сглаживания маршрута и устранения пиков. Однако для дальнейшего повышения качества алгоритма необходима дополнительная обработка последовательности координат с целью Молодежный научно-технический вестник ФС, ISSN

7 устранения избыточных точек, возникающих при отсутствии движения наблюдаемого объекта. Список литературы 1. Yadav J., Giri R., Meena L. Error handling in GPS data processing // Mausam Vol. 62. No. 1. P Kalman R. E. A New Approach to Linear Filtering and Prediction Problems // Transactions of the ASME Journal of Basic Engineering Vol. 82. No. Series D. PP Welch G., Bishop G. An Introduction to the Kalman Filter: Tech. Rep. TR Available at: accessed Vincenty T. Direct and Inverse Solutions of Geodesics on the Ellipsoid with application of nested equations // Survey Review apr. Vol. 23. No PP

УДК 519.711.2 Алгоритм оценки параметров ориентации космического аппарата с использованием фильтра Калмана Д. И. Галкин 1 1 МГТУ им. Н.Э. Баумана, Москва, 155, Россия Дано описание построения фильтра Калмана

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ НАЦИОНАЛЬНЫЙ СТАНДАРТ российской ФЕДЕРАЦИИ ГОСТ Р 53608-2009 Глобальная навигационная спутниковая система МЕТОДЫ И ТЕХНОЛОГИИ ВЫПОЛНЕНИЯ

БАЙЕСОВСКОЕ ПРОГНОЗИРОВАНИЕ ВРЕМЕННЫХ РЯДОВ НА ОСНОВЕ МОДЕЛЕЙ В ПРОСТРАНСТВЕ СОСТОЯНИЙ В И Лобач Белорусский государственный университет Минск Беларусь E-mail: lobach@bsub Рассматривается метод прогнозирования

УДК 681.5(07) ИДЕНТИФИКАЦИЯ НЕЛИНЕЙНЫХ ДИНАМИЧЕСКИХ ОБЪЕКТОВ ВО ВРЕМЕННОЙ ОБЛАСТИ Д.Н. Вятченников, В.В. Кособуцкий, А.А. Носенко, Н.В. Плотникова Недостаточная информация об объектах при разработке их

Сер. 0. 200. Вып. 4 ВЕСТНИК САНКТ-ПЕТЕРБУРГСКОГО УНИВЕРСИТЕТА ПРОЦЕССЫ УПРАВЛЕНИЯ УДК 539.3 В. В. Карелин ШТРАФНЫЕ ФУНКЦИИ В ЗАДАЧЕ УПРАВЛЕНИЯ ПРОЦЕССОМ НАБЛЮДЕНИЯ. Введение. Статья посвящена проблеме

УДК 63.1/.7 АЛГОРИТМЫ ВТОРИЧНОЙ ОБРАБОТКИ ИНФОРМАЦИИ В РАДИОЛОКАЦИОННОЙ СТАНЦИИ С РАЗЛИЧНЫМИ ВИДАМИ МАТРИЦЫ ДИНАМИЧЕСКОГО ПЕРЕСЧЕТА ПРИ ОПРЕДЕЛЕНИИ КООРДИНАТЫ УГЛА МЕСТА Яницкий А.А. научный руководитель

УДК 5979 + 5933 Г А Омарова Èíñòèòóò âû èñëèòåëüíîé ìàòåìàòèêè è ìàòåìàòè åñêîé ãåîôèçèêè ÑÎ ÐÀÍ ïð Àêàä Ëàâðåíòüåâà, 6, Íîâîñèáèðñê, 630090, Ðîññèÿ E-mail: gulzira@ravccru Статистическая модель движения

Введение в робототехнику Лекция 12. Часть 2. Навигация и картографирование. SLAM SLAM Simultaneous Localization And Mapping (одновременная локализация и картографирование) Задача SLAM является одной из

Конспект лекции «Линейные динамические системы. Фильтр Калмана.» по спецкурсу «Структурные методы анализа изображений и сигналов» 211 Ликбез: некоторые свойства нормального распределения. Пусть x R d распределен

Система локализации робота на основе полусферической камеры Александр Овчинников, Хоа Фан Кафедра Радиоэлектронники Тульский Государственный Университет, Тула, Россия [email protected], [email protected]

Труды МАИ Выпуск 84 УДК 57:5198 wwwmairu/science/trudy/ Определение погрешностей бескарданной инерциальной навигационной системы в режиме рулежки и разгона Вавилова НБ* Голован АА Кальченко АО** Московский

# 08, август 2016 УДК 004.93"1 Нормализация данных 3D камеры с использованием метода главных компонент для решения задачи распознавания поз и поведения пользователей Умного дома Малых Д.А., студент Россия,

Национальный технический университет Украины «Киевский политехнический институт» Кафедра приборов и систем ориентации и навигации Методические указания к лабораторным работам по дисциплине «Навигационные

УДК 629.78.018:621.397.13 МЕТОД ПАРНЫХ РАССТОЯНИИ В ЗАДАЧЕ ПОЛЕТНОЙ ЮСТИРОВКИ АСТРОДАТЧИКОВ СИСТЕМЫ ОРИЕНТАЦИИ КОСМИЧЕСКИХ АППАРАТОВ Б.М. Суховилов По мере улучшения точности и надежности астрономических

УДК 629.05 Решение задачи навигации с помощью бесплатформенной инерциальной системы навигации и системы воздушных сигналов Мкртчян В.И., студент, кафедра «Приборы и системы ориентации, стабилизации и навигации»

МОДЕЛЬ ЗРИТЕЛЬНОЙ СИСТЕМЫ ЧЕЛОВЕКА- ОПЕРАТОРА ПРИ РАСПОЗНАВАНИИ ОБРАЗОВ ОБЪЕКТОВ Ю.С. Гулина, В.Я. Колючкин Московский государственный технический университет им. Н.Э. Баумана, Изложена математическая

РАКЕТНО-КОСМИЧЕСКОЕ ПРИБОРОСТРОЕНИЕ И ИНФОРМАЦИОННЫЕ СИСТЕМЫ 2015, том 2, выпуск 3, c. 79 83 УДК 681.3.06 СИСТЕМНЫЙ АНАЛИЗ, УПРАВЛЕНИЕ КОСМИЧЕСКИМИ АППАРАТАМИ, ОБРАБОТКА ИНФОРМАЦИИ И СИСТЕМЫ ТЕЛЕМЕТРИИ

Линейные динамические системы. Фильтр Калмана. Ликбез: некоторые свойства нормального распределения Плотность распределения.4.3.. -4 x b.5 x b =.7 5 p(x a x b =.7) - x p(x a,x b) p(x a) 4 3 - - -3 x.5

УДК 621.396.671 О. С. Л и т в и н о в, А. А. Г и л я з о в а ОЦЕНКА С ПОМОЩЬЮ МЕТОДА СОБСТВЕННЫХ ДИАГРАММ ВОЗДЕЙСТВИЯ ГРУПП ПОМЕХ НА ПРИЕМ ПОЛЕЗНОГО СИГНАЛА ЛИНЕЙНОЙ ЭКВИДИСТАНТНОЙ АДАПТИВНОЙ АНТЕННОЙ

УДК 681.5.15.44 ПРОНОЗИРОВАНИЕ КУСОЧНО-СТАЦИОНАРНЫХ ПРОЦЕССОВ Е.Ю. Алексеева Рассматриваются дискретные случайные процессы содержащие параметры меняющиеся скачкообразно в случайные моменты времени. Для

УДК 63966 ЛИНЕЙНАЯ ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ ПРИ НЕ БЕЛЫХ ШУМАХ Г Ф Савинов В работе получен алгоритм оптимального фильтра для случая когда входные воздействия и шумы представляют собой случайные гауссовы

Определение колебательных движений нежёстких элементов спутника с помощью обработки видеоизображения Д.О. Лазарев Московский физико-технический институт Научный руководитель, к.ф.-м.н.: Д.С. Иванов, Институт

УДК 004 О МЕТОДАХ ОТСЛЕЖИВАНИЯ И ТРЕКИНГА ОБЪЕКТА НА ВИДЕОПОТОКЕ ПРИМЕНИТЕЛЬНО К СИСТЕМЕ ВИДЕОАНАЛИТИКИ ДЛЯ СБОРА И АНАЛИЗА МАРКЕТИНГОВЫХ ДАННЫХ Чезганов Д.А., Сериков О.Н. Южно-Российский государственный

Электронный журнал «Труды МАИ». Выпуск 66 www.ma.u/scence/tud/ УДК 69.78 Модифицированный навигационный алгоритм для определения положения ИСЗ по сигналам GS/ГЛОНАСС Куршин А. В. Московский авиационный

УДК 621.396.96 Исследование алгоритма завязки и подтверждения траекторий по критерию M из N Чернова Т.С., студент кафедры «Радиоэлектронные системы и устройства», Россия, 105005, г. Москва, МГТУ им. Н.Э.

ТЕОРІЯ ТА ПРАКТИКА НАВІГАЦІЙНИХ ПРИЛАДІВ І СИСТЕМ УДК 531.383 ВЛИЯНИЕ ПОГРЕШНОСТИ ПОВОРОТА СТЕНДА НА ТОЧНОСТЬ КА- ЛИБРОВКИ БЛОКА ГИРОСКОПОВ И АКСЕЛЕРОМЕТРОВ Аврутов В. В., Мазепа Т. Ю. Национальный технический

Лекция 6 Характеристики портфелей В предыдущих лекциях неоднократно употреблялся термин «портфель» Для математической постановки задачи о выборе оптимального портфеля необходимо строгое определение этого

ИДЕНТИФИКАЦИЯ ВРЕМЕННЫХ РЯДОВ С ПРОПУСКАМИ НА ОСНОВЕ МОДЕЛЕЙ В ПРОСТРАНСТВЕ СОСТОЯНИЙ Р. И. Меркулов В. И. Лобач Белорусский государственный университет Минск Беларусь e-mail: [email protected] [email protected]

ПРИБОРЫ И СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УДК 51971 В Н АРСЕНЬЕВ, А Г КОХАНОВСКИЙ, А С ФАДЕЕВ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СВЯЗИ ИЗОХРОННЫХ ВАРИАЦИЙ ПЕРЕМЕННЫХ СОСТОЯНИЯ СИСТЕМЫ УПРАВЛЕНИЯ С ВОЗМУЩЕНИЯМИ ПАРАМЕТРОВ

Труды МАИ. Выпуск 89 УДК 629.051 www.mai.ru/science/trudy/ Калибровка бесплатформенной инерциальной навигационной системы при повороте вокруг вертикальной оси Матасов А.И.*, Тихомиров В.В.** Московский

Аналитическая геометрия Модуль 1 Матричная алгебра Векторная алгебра Текст 4 (самостоятельное изучение) Аннотация Линейная зависимость векторов Критерии линейной зависимости двух, трех и четырех векторов

УДК 62.396.26 Л.А. Подколзина, К.. Другов АЛГОРИТЫ ОБРАБОТКИ ИНФОРАЦИИ В НАВИГАЦИОННЫХ СИСТЕАХ НАЗЕНЫХ ПОДВИЖНЫХ ОБЪЕКТОВ ДЛЯ КАНАЛА ОПРЕДЕЛЕНИЯ КООРДИНАТ ЕСТОПОЛОЖЕНИЯ Для определения координат и параметров

СТАТИСТИЧЕСКИЙ АНАЛИЗ ПАРАМЕТРИЧЕСКИХ ВРЕМЕННЫХ РЯДОВ С ПРОПУСКАМИ НА ОСНОВЕ МОДЕЛЕЙ В ПРОСТРАНСТВЕ СОСТОЯНИЙ С. В. Лобач Белорусский государственный университет Минск, Беларусь е-mail: [email protected]

Математичні методи обробки даних УДК 6.39 С. Я. Жук.. Кожешкурт.. Юзефович Национальный технический университет Украины «КП» просп. Победы 37 356 Киев Украина нститут проблем регистрации информации НАН

Построение ММ статики технологических объектов При исследовании статики технологических объектов наиболее часто встречаются объекты со следующими типами структурных схем (рис: О с одной входной х и одной

Оценка параметров ориентации космического аппарата с использованием фильтра Калмана Студент, кафедра «Системы автоматического управления»: Д.И. Галкин Научный руководитель: А.А. Карпунин, к.т.н., доцент

5. Мелешко В.В. Бесплатформенные инерциальные навигационные системы: Учебн. пособ. / В.В. Мелешко, О.И. Нестеренко. Кировоград: ПОЛИМЕД-Сервис, 211. 172 с. Надійшла до редакції 17 квітня 212 року ÓКостюк

УДК 004.896 Применение геометрических преобразований для анаморфирования изображений Канев А.И., специалист Россия, 105005, г. Москва, МГТУ им. Н.Э. Баумана, кафедра «Системы обработки информации и управления»

4. Методы Монте-Карло 1 4. Методы Монте-Карло Для моделирования различных физических, экономических и прочих эффектов широко распространены методы, называемые методами Монте-Карло. Они обязаны своим названием

Полосовая фильтрация 1 Полосовая фильтрация В предыдущих разделах была рассмотрена фильтрация быстрых вариаций сигнала (сглаживание) и его медленных вариаций (устранение тренда). Иногда требуется выделить

[ЗАМЕТКИ] Пояснение Основ фильтра Калмана С помощью Простого и интуитивно понятного Выведения Рэмси Фарахер та статья предоставляет Э простой и интуитивный вывод фильтра Калмана, с целью обучения этому

УДК 004.932 Алгоритм классификации отпечатков пальцев Ломов Д.С., студент Россия, 105005, г. Москва, МГТУ им. Н.Э. Баумана, кафедра «Программное обеспечение ЭВМ и информационные технологии» Научный руководитель:

Лекция ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН -МЕРНЫЙ СЛУЧАЙНЫЙ ВЕКТОР ЦЕЛЬ ЛЕКЦИИ: определить числовые характеристики системы двух случайных величин: начальные и центральные моменты ковариацию

Динамика рождаемости по Чувашской республике Содержание Введение 1. Общая тенденция рождаемости населения Чувашской республики 2. Основная тенденция рождаемости 3. Динамика рождаемости городского и сельского

IN 1990-5548 Електроніка та системи управління. 2011. 4(30) 73 УДК656.7.052.002.5:681.32(045) В. М. Синеглазов, д-р техн. наук, проф., Ш. И. Аскеров ОПТИМАЛЬНАЯ КОМПЛЕКСНАЯ ОБРАБОТКА ДАННЫХ В НАВИГАЦИОННЫХ

УДК 004.896 Особенности реализации алгоритма для отображения результатов анаморфирования Канев А.И., специалист Россия, 105005, г. Москва, МГТУ им. Н.Э. Баумана, кафедра «Системы обработки информации и

177 УДК 658.310.8: 519.876.2 ИСПОЛЬЗОВАНИЕ ТОЧНОСТИ ОЦЕНИВАНИЯ ПРИ РЕЗЕРВИРОВАНИИ ДАТЧИКОВ Л.И. Лузина В статье рассматривается возможный подход для получения новой схемы резервирования датчиков. Традиционная

СБОРНИК НАУЧНЫХ ТРУДОВ НГТУ. 28. 4(54). 37 44 УДК 59.24 О КОМПЛЕКСЕ ПРОГРАММ ДЛЯ РЕШЕНИЯ ЗАДАЧИ ИДЕНТИФИКАЦИИ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ ДИСКРЕТНЫХ СТАЦИОНАРНЫХ ОБЪЕКТОВ Г.В. ТРОШИНА Рассмотрен комплекс программ

УДК 625.1:519.222:528.4 С.И. Долганюк С.И. Долганюк, 2010 ПОВЫШЕНИЕ ТОЧНОСТИ НАВИГАЦИОННОГО РЕШЕНИЯ ПРИ ПОЗИЦИОНИРОВАНИИ МАНЕВРОВЫХ ЛОКОМОТИВОВ ЗА СЧЕТ ИСПОЛЬЗОВАНИЯ ЦИФРОВЫХ МОДЕЛЕЙ ПУТЕВОГО РАЗВИТИЯ

УДК 531.1 АДАПТАЦИЯ ФИЛЬТРА КАЛМАНА ДЛЯ ИСПОЛЬЗОВАНИЯ С ЛОКАЛЬНОЙ И ГЛОБАЛЬНОЙ СИСТЕМАМИ НАВИГАЦИИ А.Н.Забегаев ([email protected]) В.Е.Павловский ([email protected]) Институт прикладной математики им.

АВТОМАТИЗАЦИЯ И УПРАВЛЕНИЕ УДК 68.58.3 А. Г. Шпекторов, В. Т. Фам Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина) Анализ применения микромеханических

ОСНОВЫ РЕГРЕССИОННОГО АНАЛИЗА ПОНЯТИЕ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА Для решения задач экономического анализа и прогнозирования очень часто используются статистические, отчетные или наблюдаемые

Лекция 4. Решение систем линейных уравнений методом простых итераций. Если система имеет большую размерность (6 уравнений) или матрица системы разрежена, более эффективны для решения непрямые итерационные

58-я научная конференция МФТИ Секция динамики и управления движением космических аппаратов Система определения движения макетов системы управления на аэродинамическом столе с использованием видеокамеры

Лекция 3 5. МЕТОДЫ ПРИБЛИЖЕНИЯ ФУНКЦИЙ ПОСТАНОВКА ЗАДАЧИ Рассматриваются сеточные табличные функции [ a b] y 5. определенные в узлах сетки Ω. Каждая сетка характеризуется шагами h неравномерного или h

1. Численные методы решения уравнений 1. Системы линейных уравнений. 1.1. Прямые методы. 1.2. Итерационные методы. 2. Нелинейные уравнения. 2.1. Уравнения с одним неизвестным. 2.2. Системы уравнений. 1.

УДК 621.396 ИССЛЕДОВАНИЕ АЛГОРИТМОВ ВТОРИЧНОЙ ОБРАБОТКИ ИНФОРМАЦИИ МНОГОПОЗИЦИОННОЙ РАДИОЛОКАЦИОНОЙ СИСТЕМЫ ДЛЯ КАНАЛА УГЛА МЕСТА Борисов А.Н., Глинченко В.А., Назаров А.А., Исламов Р.В., Сучков П.В. Научный

Тема Численные методы линейной алгебры - - Тема Численные методы линейной алгебры Классификация Выделяют четыре основных раздела линейной алгебры: Решение систем линейных алгебраических уравнений (СЛАУ)

УДК 004.352.242 Восстановление смазанных изображений путем решения интегрального уравнения типа свертки Иванникова И.А., студент Россия, 105005, г. Москва, МГТУ им. Н.Э. Баумана, кафедра «Системы автоматизированного

АЭРОГРАВИМЕТРИЧЕСКАЯ СЪЕМКА ПРИ СТАНДАРТНОМ РЕЖИМЕ РАБОТЫ GPS Могилевский В.Е. АО «ГНПП «Аэрогеофизика» Важнейшим элементом, определяющим успех аэрогеофизических исследований, является качественное навигационное

АНАЛИЗ АКУСТИЧЕСКИХ СИГНАЛОВ НА ОСНОВЕ МЕТОДА ФИЛЬТРАЦИИ КАЛМАНА И.П. Гуров, П.Г. Жиганов, А.М. Озерский Рассматриваются особенности динамической обработки стохастических сигналов с использованием дискретных

УДК АА Минко ИДЕНТИФИКАЦИЯ ЛИНЕЙНОГО ОБЪЕКТА ПО РЕАКЦИИ НА ГАРМОНИЧЕСКИЙ СИГНАЛ Предложен алгоритм обобщенной идентификации на основе интегральных двупараметрических преобразований Гаусса линейного стационарного

ЛЕКЦИЯ. Оценка комплексной амплитуды сигнала. Оценка времени запаздывания сигнала. Оценка частоты сигнала со случайной фазой. Совместная оценка времени запаздывания и частоты сигнала со случайной фазой.

Вычислительные технологии Том 18, 1, 2013 Идентификация параметров процесса аномальной диффузии на основе разностных уравнений А. С. Овсиенко Самарский государственный технический университет, Россия e-mail:

1 ПРОГНОЗИРОВАНИЕ КОНЪЮНКТУРЫ РЫНКА НЕФТЕХИМИЧЕКСИХ ПРЕДПРИЯТИЙ Кордунов Д.Ю., Битюцкий С.Я. Введение. В современных условиях хозяйствования, которые характеризуются быстрым развитием мировых интеграционных

Задача одновременной локализации и построения карты (SLAM) Робошкола-2014 Андрей Антонов robotosha.ru 10 октября 2014 г. План 1 Основы SLAM 2 RGB-D SLAM 3 Робот Андрей Антонов (robotosha.ru) Задача SLAM

УДК 004.021 Т. Н. Р о м а н о в а, А. В. С и д о р и н, В. Н. С о л я к о в, К. В. К о з л о в СИНТЕЗ МОНОХРОМНОГО ИЗОБРАЖЕНИЯ ИЗ МНОГОДИАПАЗОННОГО ПОСТРОЕНИЕМ ПАЛИТРЫ С ПОМОЩЬЮ РЕШЕНИЯ УРАВНЕНИЯ ПУАССОНА

Национальный технический университет Украины «Киевский политехнический институт» Кафедра приборов и систем ориентации и навигации Методические указания к лабораторным работам по дисциплине «Навигационные

Цифровая Обработка Сигналов /9 УДК 69.78 АНАЛИТИЧЕСКИЙ МЕТОД РАСЧЕТА ПОГРЕШНОСТЕЙ ОПРЕДЕЛЕНИЯ УГЛОВОЙ ОРИЕНТАЦИИ ПО СИГНАЛАМ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ Алешечкин А.М. Введение Режим определения

ОСОБЕННОСТИ ФОРМИРОВАНИЯ КОМПЬЮТЕРНОЙ МОДЕЛИ ДИНАМИЧЕСКОЙ ОПТИКО-ЭЛЕКТРОННОЙ СИСТЕМЫ Позднякова Н.С., Торшина И.П. Московский государственный университет геодезии и картографии Факультет оптико-информационных

Труды ИСА РАН 009. Т. 46 III. ПРИКЛАДНЫЕ ЗАДАЧИ РАСПРЕДЕЛЕННЫХ ВЫЧИСЛЕНИЙ Стационарные состояния в нелинейной модели переноса заряда в ДНК * Стационарные состояния в нелинейной модели переноса заряда в

Винеровские фильтры лучше всего подходят для обработки процессов или отрезков процессов в целом (блочная обработка). Для последовательной обработки требуется текущая оценка сигнала на каждом такте с учетом информации, поступающей на вход фильтра в процессе наблюдения.

При винеровской фильтрации каждый новый отсчет сигнала потребовал бы пересчета всех весовых коэффициентов фильтра. В настоящее время широкое распространение получили адаптивные фильтры, в которых поступающая новая информация используется для непрерывной корректировки ранее сделанной оценки сигнала (сопровождение цели в радиолокации, системы автоматического регулирования в управлении и т.д). Особенный интерес представляют адаптивные фильтры рекурсивного типа, известные как фильтр Калмана.

Эти фильтры широко используются в контурах управления в системах автоматического регулирования и управления. Именно оттуда они и появились, подтверждением чему служит столь специфическая терминология, используемая при описании их работы, как пространство состояний.

Одна из основных задач, требующих своего решения в практике нейронных вычислений, – получение быстрых и надежных алгоритмов обучения НС. В этой связи может оказаться полезным использование в контуре обратной связи обучающего алгоритма линейных фильтров. Так как обучающие алгоритмы имеют итеративную природу, такой фильтр должен представлять собой последовательное рекурсивное устройство оценки.

Задача оценки параметров

Одной из задач теории статистических решений, имеющих большое практическое значение, является задача оценки векторов состояния и параметров систем, которая формулируется следующим образом. Предположим, необходимо оценить значение векторного параметра $X$, недоступного непосредственному измерению. Вместо этого измеряется другой параметр $Z$, зависящий от $X$. Задача оценивания состоит в ответе на вопрос: что можно сказать об $X$, зная $Z$. В общем случае, процедура оптимальной оценки вектора $X$ зависит от принятого критерия качества оценки.

Например, байесовский подход к задаче оценки параметров требует полной априорной информации о вероятностных свойствах оцениваемого параметра, что зачастую невозможно. В этих случаях прибегают к методу наименьших квадратов (МНК), который требует значительно меньше априорной информации.

Рассмотрим применения МНК для случая, когда вектор наблюдения $Z$ связан с вектором оценки параметров $X$ линейной моделью, и в наблюдении присутствует помеха $V$, некоррелированная с оцениваемым параметром:

$Z = HX + V$, (1)

где $H$ – матрица преобразования, описывающая связь наблюдаемых величин с оцениваемыми параметрами.

Оценка $X$, минимизирующая квадрат ошибки, записывается следующим образом:

$X_{оц}=(H^TR_V^{-1}H)^{-1}H^TR_V^{-1}Z$, (2)

Пусть помеха $V$ не коррелирована, в этом случае матрица $R_V$ есть просто единичная матрица, и уравнение для оценки становится проще:

$X_{оц}=(H^TH)^{-1}H^TZ$, (3)

Запись в матричной форме сильно экономит бумагу, но может быть для кого то непривычна. Следующий пример, взятый из монографии Коршунова Ю. М. "Математические основы кибернетики", все это иллюстрирует.
Имеется следующая электрическая цепь:

Наблюдаемые величины в данном случае – показания приборов $A_1 = 1 A, A_2 = 2 A, V = 20 B$.

Кроме того, известно сопротивление $R = 5$ Ом. Требуется оценить наилучшим образом, с точки зрения критерия минимума среднего квадрата ошибки значения токов $I_1$ и $I_2$. Самое важное здесь заключается в том, что между наблюдаемыми величинами (показаниями приборов) и оцениваемыми параметрами существует некоторая связь. И эта информация привносится извне.

В данном случае, это законы Кирхгофа, в случае фильтрации (о чем речь пойдет дальше) – авторегрессионная модель временного ряда, предполагающая зависимость текущего значения от предшествующих.

Итак, знание законов Кирхгофа, никак не связанное с теорией статистических решений, позволяет установить связь между наблюдаемыми значениями и оцениваемыми параметрами (кто изучал электротехнику – могут проверить, остальным придется поверить на слово):

$$z_1 = A_1 = I_1 + \xi_1 = 1$$

$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2$$

$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4$$

Это же в векторной форме:

$$\begin{vmatrix} z_1\\ z_2\\ z_3 \end{vmatrix} = \begin{vmatrix} 1 & 0\\ 1 & 1\\ 1 & 2 \end{vmatrix} \begin{vmatrix} I_1\\ I_2 \end{vmatrix} + \begin{vmatrix} \xi_1\\ \xi_2\\ \xi_3 \end{vmatrix}$$

Или $Z = HX + V$, где

$$Z= \begin{vmatrix} z_1\\ z_2\\ z_3 \end{vmatrix} = \begin{vmatrix} 1\\ 2\\ 4 \end{vmatrix} ; H= \begin{vmatrix} 1 & 0\\ 1 & 1\\ 1 & 2 \end{vmatrix} ; X= \begin{vmatrix} I_1\\ I_2 \end{vmatrix} ; V= \begin{vmatrix} \xi_1\\ \xi_2\\ \xi_3 \end{vmatrix}$$

Считая значения помехи некоррелированными между собой, найдем оценку I 1 и I 2 по методу наименьших квадратов в соответствии с формулой 3:

$H^TH= \begin{vmatrix} 1 & 1& 1\\ 0 & 1& 2 \end{vmatrix} \begin{vmatrix} 1 & 0\\ 1 & 1\\ 1 & 2 \end{vmatrix} = \begin{vmatrix} 3 & 3\\ 3 & 5 \end{vmatrix} ; (H^TH)^{-1}= \frac{1}{6} \begin{vmatrix} 5 & -3\\ -3 & 3 \end{vmatrix} $;

$H^TZ= \begin{vmatrix} 1 & 1& 1\\ 0 & 1& 2 \end{vmatrix} \begin{vmatrix} 1 \\ 2\\ 4 \end{vmatrix} = \begin{vmatrix} 7\\ 10 \end{vmatrix} ; X{оц}= \frac{1}{6} \begin{vmatrix} 5 & -3\\ -3 & 3 \end{vmatrix} \begin{vmatrix} 7\\ 10 \end{vmatrix} = \frac{1}{6} \begin{vmatrix} 5\\ 9 \end{vmatrix}$;

Итак $I_1 = 5/6 = 0,833 A$; $I_2 = 9/6 = 1,5 A$.

Задача фильтрации

В отличие от задачи оценки параметров, которые имеют фиксированные значения, в задаче фильтрации требуется оценивать процессы, то есть находить текущие оценки изменяющегося во времени сигнала, искаженного помехой, и, в силу этого, недоступного непосредственному измерению. В общем случае вид алгоритмов фильтрации зависит от статистических свойств сигнала и помехи.

Будем предполагать, что полезный сигнал – медленно меняющаяся функция времени, а помеха – некоррелированный шум. Будем использовать метод наименьших квадратов, опять же по причине отсутствия априорных сведений о вероятностных характеристиках сигнала и помехи.

Вначале получим оценку текущего значения $x_n$ по имеющимся $k$ последним значениям временного ряда $z_n, z_{n-1},z_{n-2}\dots z_{n-(k-1)}$. Модель наблюдения та же, что и в задаче оценки параметров:

Понятно, что $Z$ – это вектор–столбец, состоящий из наблюдаемых значений временного ряда $z_n, z_{n-1},z_{n-2}\dots z_{n-(k-1)}$, $V$ – вектор–столбец помехи $\xi _n, \xi _{n-1},\xi_{n-2}\dots \xi_{n-(k-1)}$, искажающий истинный сигнал. А что означают символы $H$ и $X$? О каком, например, векторе–столбце $X$ может идти речь, если все, что необходимо, – это дать оценку текущего значения временного ряда? А что понимать под матрицей преобразований $H$, вообще непонятно.

На все эти вопросы можно ответить только при условии введения в рассмотрение понятия модели генерации сигнала. То есть, необходима некоторая модель исходного сигнала. Это и понятно, при отсутствии априорной информации о вероятностных характеристиках сигнала и помехи остается только строить предположения. Можно назвать это гаданием на кофейной гуще, но специалисты предпочитают другую терминологию. На их "фене" это называется параметрическая модель.

В данном случае оцениваются параметры именно этой модели. При выборе подходящей модели генерации сигнала вспомним о том, что любую аналитическую функцию можно разложить в ряд Тейлора. Поразительное свойство ряда Тейлора заключается в том, что форма функции на любом конечном расстоянии $t$ от некой точки $x=a$ однозначно определяется поведением функции в бесконечно малой окрестности точки $x=a$ (речь идет о ее производных первого и высшего порядков).

Таким образом, существование рядов Тейлора означает, что аналитическая функция обладает внутренней структурой с очень сильной связью. Если, например, ограничиться тремя членами ряда Тейлора, то модель генерации сигнала будет выглядеть так:

$x_{n-i} = F_{-i}x_n$, (4)

$$X_n= \begin{vmatrix} x_n\\ x"_n\\ x""_n \end{vmatrix} ; F_{-i}= \begin{vmatrix} 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end{vmatrix} $$

То есть формула 4, при заданном порядке полинома (в примере он равен 2) устанавливает связь между $n$-ым значением сигнала во временной последовательности и $(n-i)$–ым. Таким образом, оцениваемый вектор состояния в данном случае включает в себя, помимо собственно оцениваемого значения, первую и вторую производную сигнала.

В теории автоматического управления такой фильтр назвали бы фильтром с астатизмом 2-го порядка. Матрица преобразования $H$ для данного случая (оценка осуществляется по текущему и $k-1$ предшествующим выборкам) выглядит так:

$$H= \begin{vmatrix} 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0.5\\ 1 & 0 & 0 \end{vmatrix}$$

Все эти числа получаются из ряда Тейлора в предположении, что временной интервал между соседними наблюдаемыми значениями постоянный и равен 1.

Итак, задача фильтрации при принятых нами предположениях свелась к задаче оценки параметров; в данном случае оцениваются параметры принятой нами модели генерации сигнала. И оценка значений вектора состояния $X$ осуществляется по той же формуле 3:

$$X_{оц}=(H^TH)^{-1}H^TZ$$

По сути, мы реализовали процесс параметрического оценивания, основанный на авторегрессионной модели процесса генерации сигнала.

Формула 3 легко реализуется программно, для этого нужно заполнить матрицу $H$ и вектор столбец наблюдений $Z$. Такие фильтры называются фильтры с конечной памятью , так как для получения текущей оценки $X_{nоц}$ они используют последние $k$ наблюдений. На каждом новом такте наблюдения к текущей совокупности наблюдений прибавляется новое и отбрасывается старое. Такой процесс получения оценок получил название скользящего окна .

Фильтры с растущей памятью

Фильтры с конечной памятью обладают тем основным недостатком, что после каждого нового наблюдения необходимо заново производить полный пересчет по всем хранящимся в памяти данным. Кроме того, вычисление оценок можно начинать только после того, как накоплены результаты первых $k$ наблюдений. То есть эти фильтры обладают большой длительностью переходного процесса.

Чтобы бороться с этим недостатком, необходимо перейти от фильтра с постоянной памятью к фильтру с растущей памятью . В таком фильтре число наблюдаемых значений, по которым производится оценка, должна совпадать с номером n текущего наблюдения. Это позволяет получать оценки, начиная с числа наблюдений, равного числу компонент оцениваемого вектора $X$. А это определяется порядком принятой модели, то есть сколько членов из ряда Тейлора используется в модели.

При этом с ростом n улучшаются сглаживающие свойства фильтра, то есть повышается точность оценок. Однако непосредственная реализация этого подхода связана с возрастанием вычислительных затрат. Поэтому фильтры с растущей памятью реализуются как рекуррентные .

Дело в том, что к моменту n мы уже имеем оценку $X_{(n-1)оц}$, в которой содержится информация обо всех предыдущих наблюдениях $z_n, z_{n-1}, z_{n-2} \dots z_{n-(k-1)}$. Оценку $X_{nоц}$ получаем по очередному наблюдению $z_n$ с использованием информации, хранящейся в оценке $X_{(n-1)}{\mbox {оц}}$. Такая процедура получила название рекуррентной фильтрации и состоит в следующем:

• по оценке $X_{(n-1)}{\mbox {оц}}$ прогнозируют оценку $X_n$ по формуле 4 при $i = 1$: $X_{\mbox {nоцаприори}} = F_1X_{(n-1)оц}$. Это априорная оценка;
• по результатам текущего наблюдения $z_n$, эту априорную оценку превращают в истинную, то есть апостериорную;
• эта процедура повторяется на каждом шаге, начиная с $r+1$, где $r$ – порядок фильтра.

Окончательная формула рекуррентной фильтрации выглядит так:

$X_{(n-1)оц} = X_{\mbox {nоцаприори}} + (H^T_nH_n)^{-1}h^T_0(z_n - h_0 X_{\mbox {nоцаприори}})$, (6)

где для нашего фильтра второго порядка:

Фильтр с растущей памятью, работающий в соответствии с формулой 6 – частный случай алгоритма фильтрации, известного под названием фильтра Калмана.

При практической реализации этой формулы необходимо помнить, что входящая в него априорная оценка определяется по формуле 4, а величина $h_0 X_{\mbox {nоцаприори}}$ представляет собой первую компоненту вектора $X_{\mbox {nоцаприори}}$.

У фильтра с растущей памятью имеется одна важная особенность. Если посмотреть на формулу 6, то окончательная оценка есть сумма прогнозируемого вектора оценки и корректирующего члена. Эта поправка велика при малых $n$ и уменьшается при увеличении $n$, стремясь к нулю при $n \rightarrow \infty$. То есть с ростом n сглаживающие свойства фильтра растут и начинает доминировать модель, заложенная в нем. Но реальный сигнал может соответствовать модели лишь на отдельных участках, поэтому точность прогноза ухудшается.

Чтобы с этим бороться, начиная с некоторого $n$, накладывают запрет на дальнейшее уменьшение поправочного члена. Это эквивалентно изменению полосы фильтра, то есть при малых n фильтр более широкополосен (менее инерционен), при больших – он становится более инерционен.

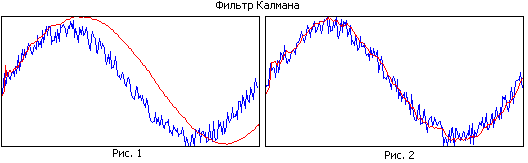
Сравните рисунок 1 и рисунок 2. На первом рисунке фильтр имеет большую память, при этом он хорошо сглаживает, но в силу узкополосности оцениваемая траектория отстает от реальной. На втором рисунке память фильтра меньше, он хуже сглаживает, но лучше отслеживает реальную траекторию.

Литература

1. Ю.М.Коршунов "Математические основы кибернетики"
2. А.В.Балакришнан "Теория фильтрации Калмана"
3. В.Н.Фомин "Рекуррентное оценивание и адаптивная фильтрация"
4. К.Ф.Н.Коуэн, П.М. Грант "Адаптивные фильтры"

Фильтр Калмана - это, наверное, самый популярный алгоритм фильтрации, используемый во многих областях науки и техники. Благодаря своей простоте и эффективности его можно встретить в GPS-приемниках, обработчиках показаний датчиков, при реализации систем управления и т.д.

Про фильтр Калмана в интернете есть очень много статей и книг (в основном на английском), но у этих статей довольно большой порог вхождения, остается много туманных мест, хотя на самом деле это очень ясный и прозрачный алгоритм. Я попробую рассказать о нем простым языком, с постепенным нарастанием сложности.

Для чего он нужен?

Любой измерительный прибор обладает некоторой погрешностью, на него может оказывать влияние большое количество внешних и внутренних воздействий, что приводит к тому, что информация с него оказывается зашумленной. Чем сильнее зашумлены данные тем сложнее обрабатывать такую информацию.

Фильтр - это алгоритм обработки данных, который убирает шумы и лишнюю информацию. В фильтре Калмана есть возможность задать априорную информацию о характере системе, связи переменных и на основании этого строить более точную оценку, но даже в простейшем случае (без ввода априорной информации) он дает отличные результаты.

Рассмотрим простейший пример - предположим нам необходимо контролировать уровень топлива в баке. Для этого в бак устанавливается емкостный датчик, он очень прост в обслуживании, но обладает некоторыми недостатками - например, зависимость от заправляемого топлива (диэлектрическая проницаемость топлива зависит от многих факторов, например, от температуры), большое влияние «болтанки» в баке. В итоге, информация с него представляет типичную «пилу» с приличной амплитудой. Такого рода датчики часто устанавливаются на тяжелой карьерной технике (не смущайтесь объемам бака):

Фильтр Калмана

Немного отвлечемся и познакомимся с самим алгоритмом. Фильтр Калмана использует динамическую модель системы (например, физический закон движения), известные управляющие воздействия и множество последовательных измерений для формирования оптимальной оценки состояния. Алгоритм состоит из двух повторяющихся фаз: предсказание и корректировка. На первом рассчитывается предсказание состояния в следующий момент времени (с учетом неточности их измерения). На втором, новая информация с датчика корректирует предсказанное значение (также с учетом неточности и зашумленности этой информации):

Уравнения представлены в матричной форме, если вы не знаете линейную алгебру - ничего страшного, дальше будет упрощенная версия без матриц для случая с одной переменной. В случае с одной переменной матрицы вырождаются в скалярные значения.

Разберемся сначала в обозначениях: подстрочный индекс обозначает момент времени: k - текущий, (k-1) - предыдущий, знак «минус» в верхнем индексе обозначает, что это предсказанное промежуточное значение.

Описание переменных представлены на следующих изображениях:

Можно долго и нудно описывать, что означают все эти таинственные матрицы переходов, но лучше, на мой взгляд, на реальном примере попробовать применить алгоритм - чтобы абстрактные значения обрели реальный смысл.

Опробуем в деле

Вернемся к примеру с датчиком уровня топлива, так как состояние системы представлено одной переменной (объем топлива в баке), то матрицы вырождаются в обычные уравнения:

Определение модели процесса

Для того, чтобы применить фильтр, необходимо определить матрицы/значения переменных определяющих динамику системы и измерений F, B и H:

F - переменная описывающая динамику системы, в случае с топливом - это может быть коэффициент определяющий расход топлива на холостых оборотах за время дискретизации (время между шагами алгоритма). Однако помимо расхода топлива, существуют ещё и заправки… поэтому для простоты примем эту переменную равную 1 (то есть мы указываем, что предсказываемое значение будет равно предыдущему состоянию).

B - переменная определяющая применение управляющего воздействия. Если бы у нас были дополнительная информация об оборотах двигателя или степени нажатия на педаль акселератора, то этот параметр бы определял как изменится расход топлива за время дискретизации. Так как управляющих воздействий в нашей модели нет (нет информации о них), то принимаем B = 0.

H - матрица определяющая отношение между измерениями и состоянием системы, пока без объяснений примем эту переменную также равную 1.

Определение сглаживающих свойств

R - ошибка измерения может быть определена испытанием измерительных приборов и определением погрешности их измерения.

Q - определение шума процесса является более сложной задачей, так как требуется определить дисперсию процесса, что не всегда возможно. В любом случае, можно подобрать этот параметр для обеспечения требуемого уровня фильтрации.

Реализуем в коде

Чтобы развеять оставшиеся непонятности реализуем упрощенный алгоритм на C# (без матриц и управляющего воздействия):

class KalmanFilterSimple1D
{
public double X0 {get; private set;} // predicted state
public double P0 { get; private set; } // predicted covariance

Public double F { get; private set; } // factor of real value to previous real value
public double Q { get; private set; } // measurement noise
public double H { get; private set; } // factor of measured value to real value
public double R { get; private set; } // environment noise

Public double State { get; private set; }
public double Covariance { get; private set; }

Public KalmanFilterSimple1D(double q, double r, double f = 1, double h = 1)
{
Q = q;
R = r;
F = f;
H = h;
}

Public void SetState(double state, double covariance)
{
State = state;
Covariance = covariance;
}

Public void Correct(double data)
{
//time update - prediction
X0 = F*State;
P0 = F*Covariance*F + Q;

//measurement update - correction
var K = H*P0/(H*P0*H + R);
State = X0 + K*(data - H*X0);
Covariance = (1 - K*H)*F;
}
}

// Применение...

Var fuelData = GetData();
var filtered = new List();

Var kalman = new KalmanFilterSimple1D(f: 1, h: 1, q: 2, r: 15); // задаем F, H, Q и R
kalman.SetState(fuelData, 0.1); // Задаем начальные значение State и Covariance
foreach(var d in fuelData)
{
kalman.Correct(d); // Применяем алгоритм

Filtered.Add(kalman.State); // Сохраняем текущее состояние
}

Результат фильтрации с данными параметрами представлен на рисунке (для настройки степени сглаживания - можно изменять параметры Q и R):

За рамками статьи осталось самое интересное - применение фильтра Калмана для нескольких переменных, задание взаимосвязи между ними и автоматический вывод значений для ненаблюдаемых переменных. Постараюсь продолжить тему как только появится время.

Надеюсь описание получилось не сильно утомительным и сложным, если остались вопросы и уточнения - добро пожаловать в комментарии)